福建省福州市福清融城中学  韩珠文  350300

摘要：数学是高中阶段需要学习的重要学科，而函数是这门学科的重要内容，所以在具体的教学中，无论是老师的教学强调还是学生的学习侧重，函数都是重头戏。具体分析函数的学习，其不仅要掌握科学的方法，更要有科学的思维，这样，学习才能实现事半功倍。化归思想是高中数学函数学习中需要利用的重要思想，此思想的利用能够将复杂的学习内容简单化，从而提升学生的学习效率。本文就数学学习中化归思想的具体实践做分析和讨论，旨在为学生的学习提供指导。

关键词：高中数学；函数学习；化归思想

    从目前的高中数学教学来看，教学不仅仅要帮助学生掌握正确的学习方法，更要帮助其建立科学的学习思维，因为数学是逻辑性比较强的学科，思维跟不上，即使掌握方法，学习成效也不会太高，所以在当前的数学教学中，更多的老师会在实践教学中强调对学生数学学习思维的培养。化归思想是数学学习中的重要思想理念，在函数问题的解决中发挥着重要的作用，具体分析此种思想的利用实践，从实践分析的角度出发帮助学生构建数学学习的科学思维，这对于高中数学函数教学效果的综合提升有重要的意义。

一、化归思想的概述

化归不仅是一种重要的解题思想，也是一种最基本的思维策略，更是一种有效的数学思维方式。所谓的化归思想方法，就是在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化，进而达到解决的一种方法。一般总是将复杂问题通过变换转化为简单问题；将难解的问题通过变换转化为容易求解的问题；将未解决的问题通过变换转化为已解决的问题。

对目前数学的学习做具体的分析，化归在数学解题中几乎无处不在，其基本功能是：生疏化成熟悉，复杂化成简单，抽象化成直观，含糊化成明朗。说到底，化归的实质就是以运动变化发展的观点，以及事物之间相互联系，相互制约的观点看待问题，善于对所要解决的问题进行变换转化，使问题得以解决。实现这种转化的方法有：待定系数法，配方法，整体代入法以及化动为静，由抽象到具体等转化思想。

二、高中数学函数学习中化归思想的应用

    在高中数学函数的学习中，化归思想的利用具有突出的效果。具体分析这种思想的利用实践可以让更多的学生了解到此种思想在函数学习中的优势，从而实现化归思想的推广和利用普及。

（一）转化未知问题为已知问题

化归思想在高中数学函数中的突出应用体现在转化为知问题为已知问题。所谓的位置问题转化为已知问题主要指的是利用公式、概念以及定理等将未知的内容或者是函数形式转变为已知的，比较熟悉的函数形式，这样，问题的解决会更加的简单。以下是转化位置问题为已知问题的案例分析。

例1：求函数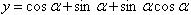的最值。

   学生拿到题目一看，该题目与已知的函数形式不一样，所以这对于学生来讲是未知的问题。但是通过转化，这个题目可以转变为学生熟悉的知识，这样，该问题的解决会更加的简单。比如在该题目的解决中可以使用换元代入法，设A=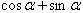，那么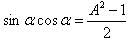,如此，原方程便成了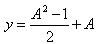,对转化后的方程进行分析发现其是一个典型的二次函数问题，此时根据二次函数的最值求解方法便可以获得该方程的最值。

    从上述问题的分析可知，通过化归思想的利用将未知的问题转化成已知的内容，这样，学生问题解决的准确性得到提升，其学习的自信心也会明显的加强。

（二）转换正面问题和反面问题

化归思想在高中函数教学中的具体利用还体现在正面问题向反面问题的转换方面。从具体的分析来看，一些函数问题从正面进行解决往往更加的复杂，而从反面做思考，下手会更加简单，所以在正面函数解决比较困难的时候，利用化归思想将其转化为反面问题，解题的效果会更加的突出。以下是具体的实例。

例2：若对于任意t∈[1,2]，且函数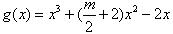在区间（t，3）总不为单调函数，则m的取值范围是？

    对该题目进行分析，发现“总不为”单调函数是明显的正面问题表述，此问题的解决从正面无法下手，所以讨论其单调函数，那么最终结果的反面就是需要解决的问题。基于此对该函数做单调性讨论则会发现g’(x)≥0在（t，3）上恒成立或者是g’(x)≤0在（t，3）上恒成立，则原函数为单调性函数。基于单调性函数问题的解决方法得出m的取值，然后确定其不满足单调性函数m的取值，这样，具体的问题便得到了解决。

（三）将函数问题转换为几何问题

    化归思想在高中函数中的具体应用还体现在函数问题向几何问题的转化方面。分析具体的函数可知，部分特殊函数的具体解决方法比较的困难，而且在解决中的出错率比较高，这对于学生的学习帮助十分不利。函数的几何图像具有直观性特点，所以利用化归思想将传统的函数转化为图像，这样，问题的解决会更加的简单。简言之，数形结合是当前高中数学函数学习中的重要利用思想，所以在准确的利用此思想进行问题的简单化处理，数学学习的效率会更高，学生学习数学的动力和积极性会更强。

结语：

    综上所述，高中的数学学习必须要有科学正确的思维方式和方法，这样，具体的学习才会更具效率。而当前的高中函数学习，很多学生没有很好的运用化归思想，所以在问题解决中出现了效率不高、错误突出的问题。针对此问题，基于实践强调化归思想的具体应用，这对于改善当前的学生数学函数学习状态问题有重要的帮助，对于教学整体性提升也有突出的意义。

参考文献：

[1]宋扣兰.化归思想在高中数学函数教学中的运用[J].中学生数理化(教与学),2016(3).

[2]甘甜.化归思想在高中数学函数学习中的运用[J].农家参谋,2017(16):78-78.

[3]廖国庆.化归思想在高中数学函数学习中的运用[J].新教育时代电子杂志:教师版,2017(47).

[4]宋宁.化归思想在高中数学函数学习中的运用[J].情感读本,2017(33):38-38.