王强 福建省福清融城中学
摘 要 如果说高中数学核心概念是一座堡垒，那么，我们就要从多个角度对这座堡垒进攻。从这个方向攻不进去，就换一个方向。一定要拿下这一座座堡垒，你的面前才会出现一片坦途。形成高中数学核心概念的学习障碍的原因是多种多样的，有方法、态度、智力和环境等方面的，但这种障碍可以通过教师和学生本人采取一定方法和对策来解决。
关键词 高中数学；核心概念；学习障碍；教师的对策；
美国教育心理家布鲁纳说：“掌握一门学科就是要掌握这门学科核心的、根本的概念。”数学家波利亚在“如何解题”中说“当你不能解决一个问题时,不妨回到定义上去”。可见，概念在数学这门学科中有着举足轻重的作用，特别是核心概念课教学效果必须要引起师生的共同关注。
一、教高中数学核心概念的过程，要有足够的停留和探究
有的高中学生认为，解题就靠公式与技巧，与概念无关，学生的这种思维习惯与观念是造成高中数学核心概念学习障碍的最基本原因。事实上我们解题的每个步骤都是对高中数学核心概念掌握程度的一次考查，基础知识扎实的同学，才能形成正确的核心概念，在解题时才可以得心应手，迎刃而解。李邦河院士：“数学根本上是玩概念的，不是玩技巧，技巧不足道也！”，而我们知道“信念和概念的改变是缓慢的。”[1], 因此我们在高中数学核心概念的教学上要肯耗费一定时间、精力，这是教数学的正轨。
针对学生的这种思维习惯与观念，教师的对策是：在教高中数学核心概念时要充分暴露核心概念的形成过程，并且在核心概念的形成过程中，教师得有足够的停留和探究，复杂的高中数学核心概念不能过于简单化处理。高中数学核心概念通常是章节的起始课，好的开头是成功的一半。教师在教学之前要在自己的脑海里勾画出本节课的线条：知识线条、知识形成线条、思维线条。其中知识的形成线条是高中数学核心概念如何生成的细微深入过程，是最核心的一个环节，然后就是考虑如何从学生的认知特点出发科学、有效地进行课堂教学。
在函数单调性的教学中，我是这样设计知识形成线条来达成核心概念的，取得了不错的效果。
教师：大家认真细致地观察函数f(x)=x2图像，我们会发现图像在y轴的右边是呈上升趋势的，而在左边呢？图像是呈下降的趋势，请大家想想我们应该怎样利用x与f(x)函数值的变化来描述函数关系呢？若我们用数学符号语言来描述函数f(x)=x2的这种上升或下降的变化规律，我们该怎么来叙述呢？
学生：在y轴的右边，函数f(x)=x2图像呈上升趋势，表格中，函数值y随着自变量x的增大也是在增大，在y轴的左边，函数f(x)=x2图像呈下降趋势，表格中，函数值y随着自变量x的增大却是在减少的。
教师：给定的函数若具有像这种的特征，那我们就称该函数具备单调性。这时我们把函数单调递增时称之为增函数，而函数单调递减时则称之为减函数。请大家思考：给定的一个函数y=f(x)，若其定义域是I，那么这个函数在某个子区间D上，我们应该如何来定义其是增函数还是减函数呢？
学生甲：我们可以通过观察函数的图像，若函数图像在区间D上如果呈上升趋势就说明它是增函数。
教师追问：那如果函数图像我们无法得到呢？
学生乙：若函数f(x)的值在区间D上随x的增大而增大，则就称f(x)在区间D上为增函数。
教师：很好，现在我们能不能更准确点来描述呢？
我们在探究如何将文字语言转化为用数学语言表达时，那么单调性的定义就能够唾手可得了。
教师要在“形成函数单调性定义”这里有足够的停留和探究，要充分暴露概念的形成过程，高中数学核心概念的教学应当重视停留和探究，高中数学核心概念的教学必须重视停留和探究。因为停留和探究刻录艰辛；因为停留和探究产出成果；因为停留和探究展现方法；因为停留和探究孕育能力。
二、教高中数学核心概念的本质属性，要联系生活和创设情境
在高中数学核心概念的教学实践中，有时我们会采用“一个定义，几项注意”的方式，即采取“概念说明+例题+考试”的“灌输”教学方法，以解题教学代替核心概念教学的做法，事实上这严重偏离了数学的正轨，必须纠正。高中数学核心概念本身是高度概括的、是高度抽象的，教师在引入阶段不能不交代为什么要探究这个核心概念，就要他们学习。教师的这种教法和观念会影响学生在学习核心概念上的效率，自然就造成了核心概念学习上的障碍。
因此教师的对策是：将教材生活化、事例化，创设情境。通过高中数学核心概念与实践的结合以激发学生学习数学的兴趣。弗兰登塔尔说：“数学是充满着联系的，如果要教学，就应该将数学学习与其有关的生活和实际内容联系起来教学。”，我们学习高中数学核心概念也需要与身边的事物还有我们的日常生活联系，并且我们引入的生活经验上的素材要与高中数学核心概念的本质属性相联系。因为高中数学核心概念对于学生来说比较抽象、比较难懂，所以我们选取与之有关的生活素材，能够建立亲切感，产生吸引力，使我们的核心概念教学相互贯通，收到事半功倍的效果，同时学生也会感觉数学来源于生活又服务于生活。
比如为什么在解析几何的圆锥曲线中教材选择椭圆的学习？学习椭圆与我们的实际生活有什么关系？在椭圆这个核心概念的教学中，我是这样设计的：
教师：假如你是一个有心人，你会发现椭圆在我们的生活中是经常可以看到的一种曲线，谁能举出一些例子来？
学生：美式足球——美式橄榄球；鸡蛋、鸭蛋；我们的人造卫星运行轨道等。（事实上椭圆在实际生活中比比皆是，但学生不一定能够留意到）教师通过引导激发了学生主动参与教学活动的热情，集体探讨后发现我们身边存在着许许多多的椭圆，这样就能够唤起学生对椭圆陌生概念的学习兴趣。
接下来请学生拿出他们课前已准备好的纸板、细绳和图钉, 利用动手实验创设合作性情境，给学生以探索的机会，激发创造的热情，我先用多媒体课件演示如何画椭圆，再让学生独立完成，使其感受成功的愉悦，然后以通过小组来回答设计的问题：
（1）椭圆是在纸板上作出的作图表明了什么?
（2）在试验过程中，什么是不变的，什么是变化的？
（3）给你同样的工具，你画出的图形一定是椭圆吗？
（4）讨论概括椭圆上的点满足什么条件？
学生在力所能及的发现中可以得出：两个定点，绳长不变（即轨迹上与两个定点距离之和不变）
当两定点的距离等于绳长时，所得轨迹是线段；当两定点的距离大于绳长时，画不出图形。
如此，椭圆定义的得出就是信手拈来的事情了。
这样的教学在实际中受到了同学们的热烈欢迎。同学们说，这样好处多多。一是觉得数学真有用，能解决实际问题；二是让他们从中体验抽象的数学核心概念数学家是如何概括出来的，最重要的是他们突破了高中数学核心概念学习的障碍。《数学新课程标准》指出：“动手实践,自主探索与合作交流是学生学习数学的重要方式” [2]，学生间的交流与合作，不仅是检验、纠正和完善知识的需要，也是培养学生表达自己观点和倾听别人意见能力的需要。
三、教高中数学核心概念的方法，要善于研讨质疑
我们谈创新意识，我认为最关键的是培养学生及时发现问题，善于捕捉问题的能力。而恰恰在造成高中数学核心概念的学习障碍的各种原因中，最主要的障碍就是学生提出问题、质疑的能力。
因此教师的对策是：在制定教学目标、教学方法选择、教学过程设计及教学效果评价等环节上都要紧紧围绕核心概念这一“灵魂”展开，通过流畅、有效、典型的“研讨质疑”，提高学生思维质量。
创设质疑性问题是指教师用新颖的方式，生动的语言设置一些使学生欲答不能，但又能通过学生自己独立思考、判断，提出自己独特的见解，产生一种新颖、独到的前所未有的问题来认识事物，从而在一定程度上推动了学生的理解与思维的发展。[3] 古人云：“学起于思，思源于疑。”学生有了疑问才会激发他们的学习热情，才有可能消除数学核心概念学习中的障碍，才会有所发展, 进而有所创造。因此，在教高中数学核心概念中要创设质疑性问题，激活他们的好奇心，吸引他们的注意力，犹如一部优秀的电视剧，让人流连忘返、欲罢不能。并且鼓励学生大胆质疑、发问，这样有利于学生消除核心概念的学习障碍。
比如：在说完双曲线定义后我出了一道这样的练习题：
双曲线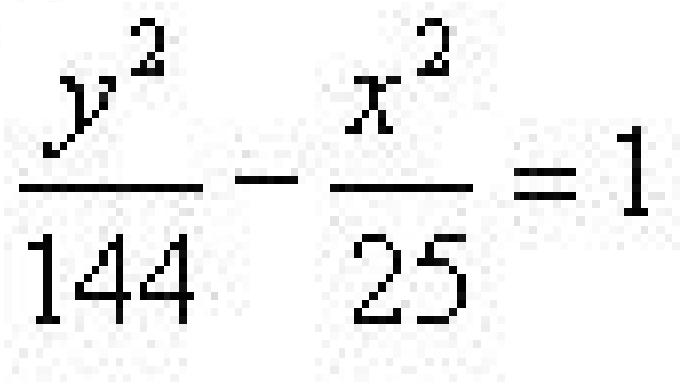
上的p到上焦点的距离为6，以下选项中正确的为（ ）
A.点P到其下焦点的距离是10； B.点P到其下焦点的距离不唯一；
C.点P到其下焦点的距离是16； D.不存在这样的点P.
有一部分学生得出如下解法：
解：设F1，F2分别为双曲线上、下焦点，依据双曲线定义可得：||PF1|-|PF2||=10
∵|PF2|=6，∴|PF1|=|PF2|+10=16，∴选C
教师：这样的解法是有误的，问题出现在哪里呢？
学生们迷惑不解，孔子曰：“不愤不启，不悱不发”，此时可提醒学生关注三角形，引导他们进行讨论发现：若|PF1|=16，则三角形两边的和|PF1|+|PF2|=22，而第三边|F1F2|=2c=26，会有|PF1|+|PF2|<|F1F2|，出现三角形两边之和小于第三边的错误，可见这样的解法确实有误，因此，本题应选D。
在教双曲线这一核心概念方法的设计上，重点放在质疑上，犹如一江春水，有认知的冲击、有思维的展开、有引人入胜的曲径。学生就能自己得出：考虑双曲线定义|PF1|-|PF2|=±2a,还要注意隐含的条件c>a和|F1F2|≤|PF1|+|PF2|。在数学课堂的学习中，做题不是目的，而是手段，做题是为了达到对核心概念更深的理解，让学生从“陷阱”中跳出来，积累抵御“陷阱”的经验，这样我们的核心概念的学习就水到渠成，自然而然了。
四、教高中数学核心概念的内在人文价值，要善于抓住时机
“建构主义的认知是以情境为动力，由学习者主动建构的，是情境与认知的融合”[4]。教师在科学把握教学内容的同时，要不失时机地引导学生去体会高中数学核心概念中丰富的人文因素，来充实学生的人文内涵，提升学生的人文品位。如解析几何之父笛卡尔的趣闻轶事让学生认识平面直角坐标系的建立；
当学生对数学中的向量与物理中的矢量为同一概念感到好奇时，不必急于解释，而可以让学生打一成语“有的放矢”去体味内中的联系。
“教师对每一个细节或一个问题的恰当的选择和精彩的讲解，对一个命题的优美的证明，或把一个枯燥的公式化成优美的形式，也能唤起学生的美感。”[5]
因此教师的对策是：在高中数学核心概念教学中既要注重数学的科学价值，也要很好地发挥概念本身所固有的人文价值功能，必能极大地激发学生学习的热情，消除高中数学核心概念学习的障碍。
比如在学习数列、等差数列、等比数列概念时，我用著名的斐波那契数列、高斯求和故事还有棋盘放麦粒问题导入，让他们体会到古今中外数学家在事业上的孜孜不倦、锲而不舍；在治学上的勤奋刻苦、严谨认真；在品行上的刚正不阿、诲人不倦。既帮助学生更深刻地理解了这些核心概念，又体验探索到了高中数学核心概念的内在美。
概念模糊，学习糊涂，数学家王元说：“学习数学首先要弄清一个个概念，否则脑子里难免是一盆浆糊。”，可见掌握高中数学核心概念是学好高中数学的前提和基础。核心概念学习中的夹生饭，会让学生无法逾越概念学习中的障碍，可能导致高中数学学习的失败。概念不清则思路不通，若只是大量的做题，不可能提高对高中数学核心概念的本质理解，反而会增加厌恶。因此，教师要摒弃实用主义，真正领悟数学核心概念的价值。总之，千重要，万重要，吃透教材最重要；千般好、万般好，抓住核心概念才最好；这个法，那个法，不抓核心概念不得法。
参考文献
[1][美]D.A.格劳斯主编.陈昌平等译《数学教与学研究手册》，上海教育出版社，1999。
[2]数学课程标准研制组.《普通高中数学课程标准(实验)解读》，江苏教育出版社,2004。
[3]周军.《教学策略》，教育科学出版社，2003。
[4]郑毓信.《数学教育从理论到实践》，上海教育出版社，2001。
[5]代钦.《健康的个性与数学教育的相互作用》，内蒙古师大学报(自然科学汉文版)，1992